Interpret Federated Learning with Shapley Values

In this paper authors investigate the model interpretation methods for Federated Learning, specifically on the measurement of feature importance of vertical Federated Learning where feature space of the data is divided into two parties, namely host and guest. For host party to interpret a single prediction of vertical Federated Learning model, the interpretation results, namely the feature importance, are very likely to reveal the protected data from guest party. Aunthors propose a method to balance the model interpretability and data privacy in vertical Federated Learning by using Shapley values to reveal detailed feature importance for host features and a unified importance value for federated guest features. Authors’ experiments indicate robust and informative results for interpreting Federated Learning models.

Shapley value

We know that many machine learning models are black box or semi-black box models. If the model is used for perception tasks such as speech recognition and image recognition, people may not be too concerned about the interpretability of the model. Many people remember the example of the panda that is recognized as a growth arm, but these jobs may be more from the perspective of model reliability.

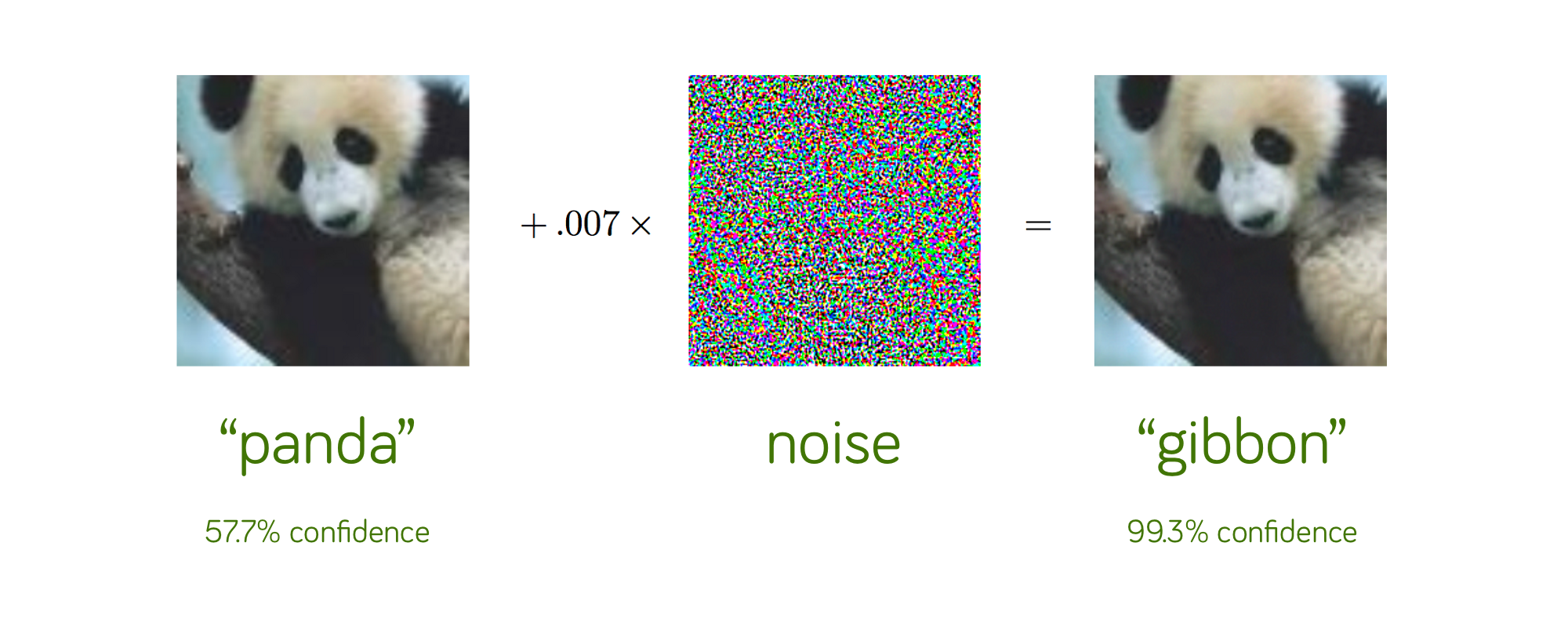
The model’s interpretability is especially important for non-perceived machine learning models in other critical applications, such as loan risk estimation, insurance underwriting forecasting, fraud identification models, and so on. An open source project on Github mentions a very interesting model-independent model interpretation method that uses Shapley values to calculate the importance of model features. It is also an important idea behind the SHAP toolkit. SHAP has been used in many practical work by a number of colleagues who are working on financial and insurance machine learning models.

We assume that a model $f(x)$ has been trained to map the feature vector $x$ to a predicted value $y$, where $x$ contains n different features, $x = {x_1, x_2, ..., x_n}$. We want to know how each feature plays in this model. This involves two levels: (1) we can be interested in each individual prediction, trying to explain each particular decision with the importance of the feature; (2) we can also be interested in the whole model, want to know each The importance of features when the model makes a large number of decisions. For the latter, which is the characteristic importance of the entire model, in fact, a toolkit such as xgboost already contains similar functions. SHAP is more focused on the former.

The Shapley value is derived from game theory, and the authors subtly apply the shapley value to model interpretability. Given a model $f$, for a particular decision, assume that specific values for all features ${x_1, x_2, ..., x_n}$ exist. We treat each feature as a switch and try to construct a series of simulated feature values. Each time, some of the features in ${x_1, x_2, ..., x_n}$ are “turned on” and “turned off”, and then the deviation between the predicted result and the original result is calculated. When we try all the possible combinations of “on” and “off”, there is a series of such deviations. We now need to calculate the importance of the feature $x_i$. As long as we refer to all the feature combinations except $x_i$, the average fluctuation of the original result is better for both cases of $x_i$ off and on.

Explaining vertical federated learning

For the vertical federated learning model established by A and B, imagine that we want to explain the model from the perspective of A. We naturally hope that the importance of all the features that A possesses can be displayed as accurately and as accurately as possible. Because A can’t get the eigenvalue of B, we hope that we can combine all the features of B into a whole feature, we call it the federated feature, and then calculate the weight value of the federated feature of B.

The author no longer simply arranges all the features of A and B, but arranges and combines all the features of A and the federated features of B, and then calculates the Shapley values of these features. The author hopes to accurately find the feature weight of A, and also has an overall understanding of B’s feature weight.

The author looks for a public dataset to experiment with, and the dataset is used to predict whether a person rich. Features include age, gender, ethnicity, country, educational information, investment income over the past year, job rating, position, and weekly working hours. We use the Shapley value to first calculate the weight values for all features as a Ground Truth reference. Then, the vertical federated learning is simulated, and the three work-related features are calculated as weights of the federated features of B, and compared with Ground Truth. We add five features of investment results and work-related features as the federated features of B, and compare them again when the federated features occupy more feature space.

🔗The code is available at https://github.com/crownpku/federated_shap

🔗Paper