Dominant Dataset Selection Algorithms for Time-Series Data Based on Linear Transformation
Published in IEEE Internet of Things Journal, 2019
Abstart
With the explosive growth of time-series data, the scale of time-series data has already exceeds the conventional computation and storage capabilities in many applications. On the other hand, the information carried by time-series data has high redundancy due to the strong correlation between time-series data. In this paper, we propose the new dominant dataset selection algorithms to extract the dataset that is only a small dataset but can represent the kernel information carried by time-series data with the error rate less than {\epsilon}, where {\epsilon} can be arbitrarily small. We prove that the selection problem of the dominant dataset is an NP-complete problem. The affine transformation model is introduced to define the linear transformation function to ensure the selection function of dominant dataset with the constant time complexity O(1). Furthermore, the scanning selection algorithm with the time complexity O(n2) and the greedy selection algorithm with the time complexity O(n3) are respectively proposed to extract the dominant dataset based on the linear correlation between time-series data. The proposed algorithms are evaluated on the real electric power consumption data of a city in China. The experimental results show that the proposed algorithms not only reduce the size of kernel dataset but ensure the time-series data integrity in term of accuracy and efficiency.
Introduction
With the popularity of smart devices and mobile phones, the time-series data (TSD) is widely generated by Internet of Things (IoT). The dynamical and rapid massive data generation in the form of TSD is highly timesensitive. Facing with the continuous arrival of TSD stream, the information processing systems need to efficiently extract the kernel data from massive data in real-time. The efficient data extraction from large-scale TSD has become an important issue in IoT industries. The conventional data extraction methods are generally based on the assumption of infinite computing and storage resources. For example, the approximate information extraction method using the summary data structure and the dimensional decomposition/recovery methods mainly focus on reducing the time complexity of algorithms. However, these existing methods fail to be appropriate for TSD with the large-scale, low-value density, and strong correlation characteristics. Therefore, the more efficient data extraction methods are expected to process massive TSD.
Definitions
Dominant Dataset:Assuming that is a finite time-series dataset, and let be another dataset, . If there is a reduction function during the time period that can meet the requirement of and , is defined as a dominant dataset of based on the function .
()-solver: Given the parameters () and (), the function is established by the correlation between the sample objects in . A small dataset can be selected as a dominant dataset of by the function such that the information representation problem of can be solved in the small dataset instead of under the condition that the probability of information extraction error being larger than is less than . This solution condition of dominant dataset selection problem is defined as ()-solver. If = 0, it means that the information extraction error is less than . In such case, the solution condition is defined as -solver.
Correlation Distance): In order to measure the degree of correlation between and , the correlation distance between and is defined as . Based on ()-solver, an element of dominant dataset can be determined by whether can be met. Note that the correlation distance holds the commutative property, that is, .
Methods
- Datasets
| Dataset | Users(n) | Days(m) | Data records(thousand) | Description |
|---|---|---|---|---|
| DS0 | 1032 | 21 | 21.672 | 21-day consumption data for each user |
| DS1 | 3000 | 7 | 21.000 | 7-day consumption data for each user |
| DS2 | 6000 | 7 | 42.000 | 7-day consumption data for each user |
| DS3 | 9000 | 7 | 63.000 | 7-day consumption data for each user |
| DS4 | 12000 | 7 | 84.000 | 7-day consumption data for each user |
- Affine Relation Model
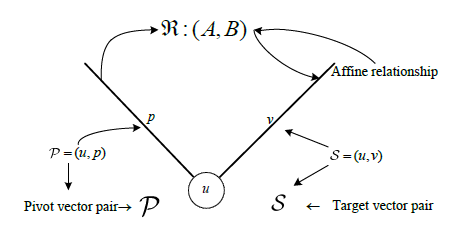
Assuming that the central object dataset and the sample object dataset , the two linear distance measures are introduced as follows:
(1)Affine linear correlation distance (AFF):
(2)Least-squares linear transformation distance (LS):
- Dominant Dataset Selection Aldorithms
(1)Scanning Selection Algorithm (SSA)

A sample for the dominant dataset selection process based on SSA:
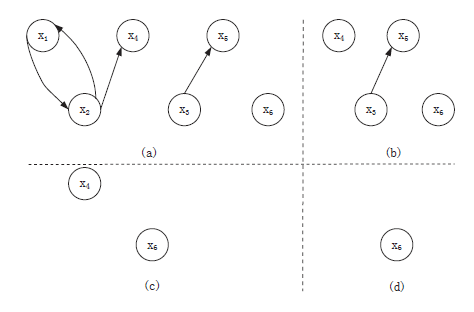
The total time complexity of SSA is O(m*n)+O(n^3), namely, O(n^3).
(2)Greedy Selection Algorithm (GSA)
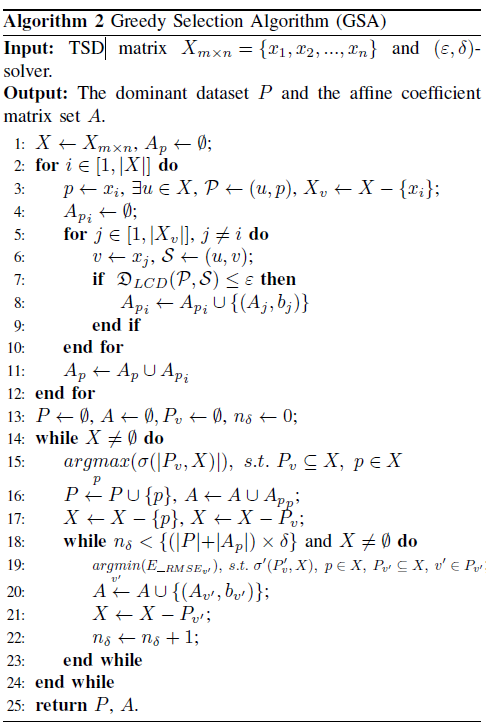
A sample for the dominant dataset selection process based on GSA:
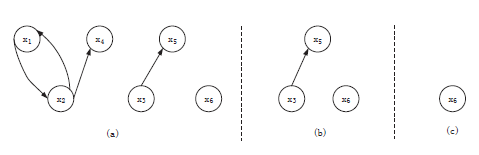
The total time complexity of GSA isO(m*n) + O(n^3) + O(n^4), namely, O(n^4).
Results
- Effects of Parameter on the Dominant Dataset Selection
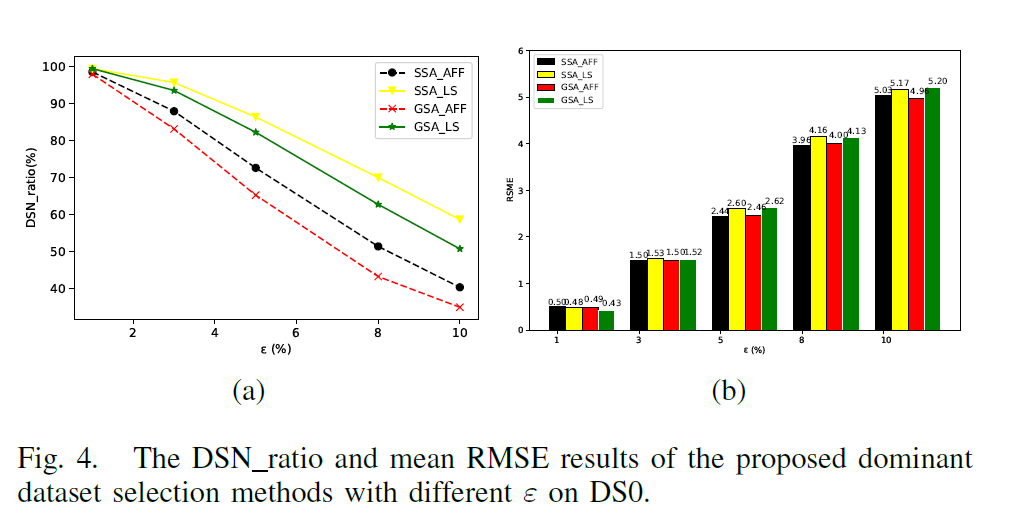
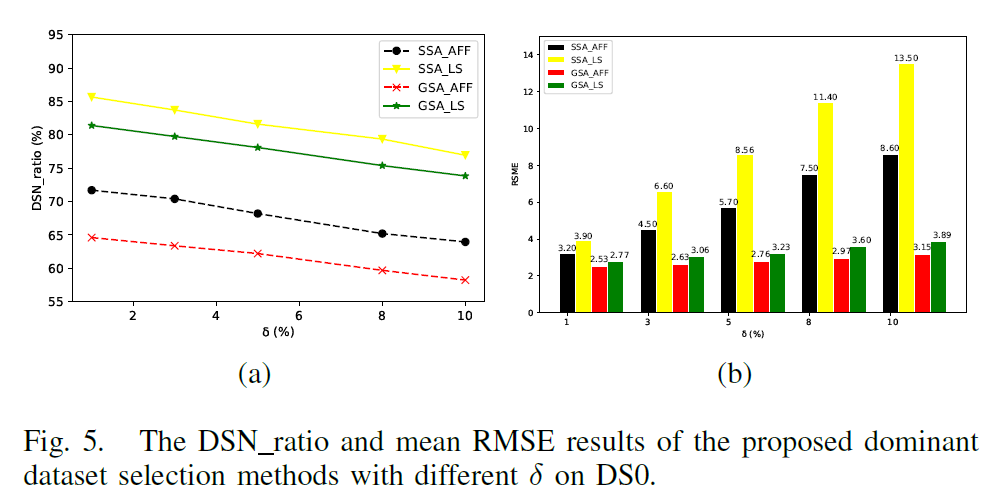
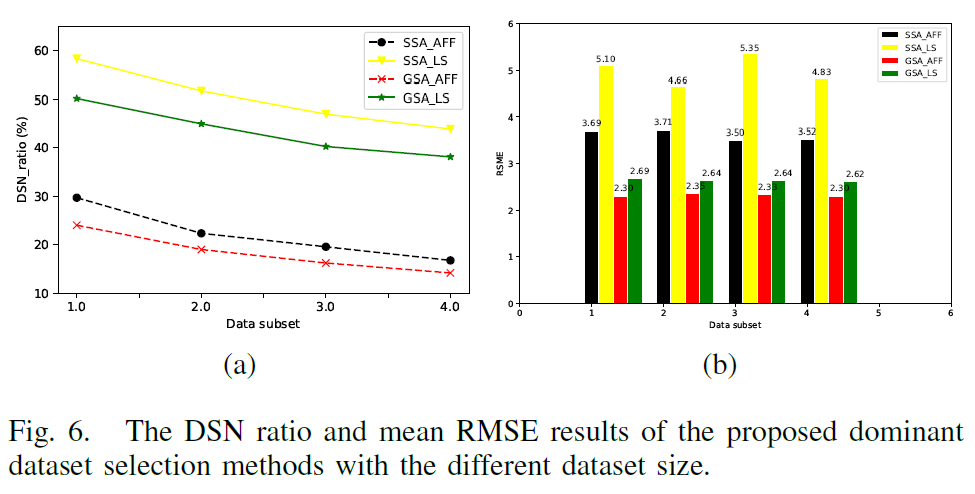
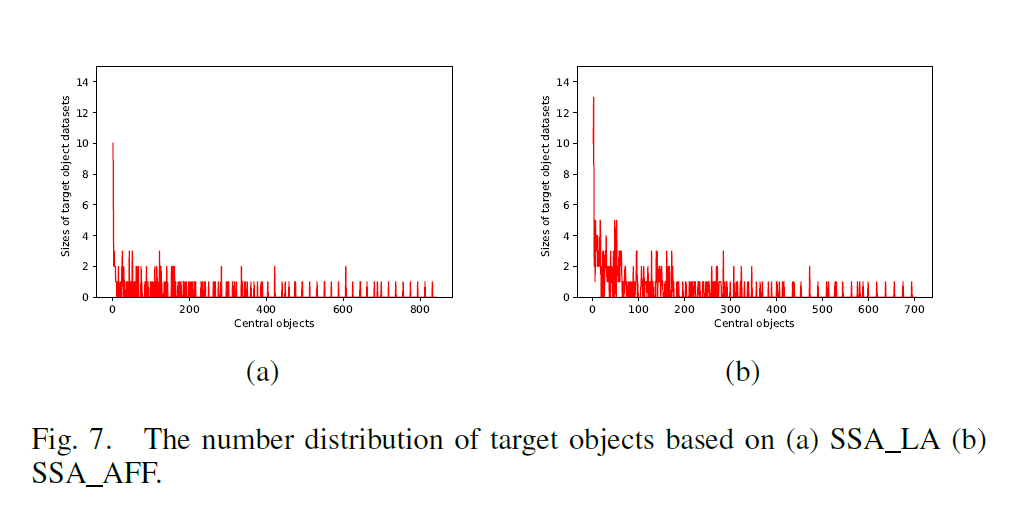
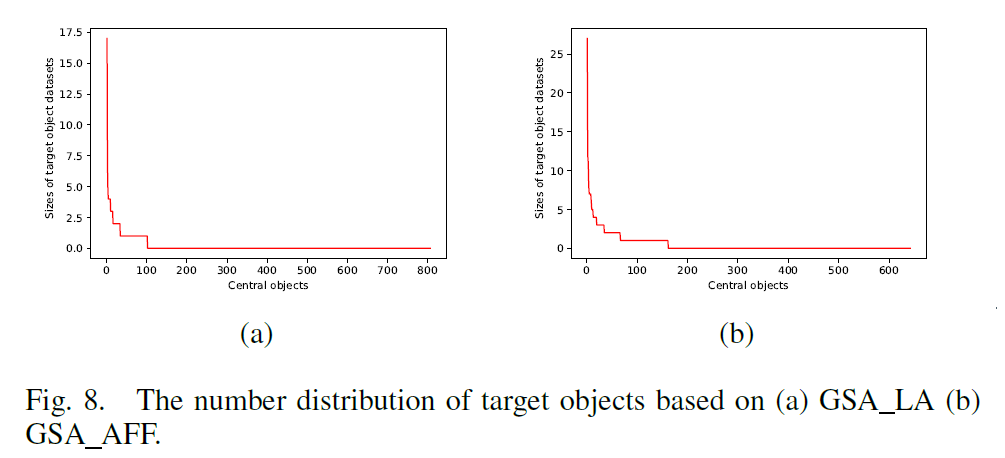
- The number distribution of target objects
CONCLUSION
This paper studies how to extract the dominant dataset from time-series data. We prove that the selection problem of the minimum dominant dataset is an NP-complete problem. Based on the linear correlation relationship between time-series data objects, we present a recursive affine transformation function to realize the efficient dominant dataset selection. In addition, the linear correlation distance is applied as the constraint condition for the dominant dataset selection. We further propose the dominant dataset selection algorithms based on the scanning strategy and the greedy strategy. The analysis and experimental results show that the proposed algorithms have high performance in terms of effectiveness and efficiency. In the future, we will continue to investigate the dominant dataset selection methods based on some linear/nonlinear relation models between time-series data, and further evaluate the proposed methods using the different types of time-series data on multiple application scenarios.